目录

一.问题引入

二.线段树

1.什么是线段树

2.线段树的举例

三.构建线段树

1.思路分析

2.代码实现

四.更新

1.思路分析

2.代码实现

五.查询

1.思路分析

2.代码实现

---

一.问题引入

有n个整数的数组,我们要 求解下标从left到right的元素之和为多少(query操作),然后还需要更新下标为index的值改为val(update操作),这个时候的时间复杂度为多少.

方法一:对于第一个问题(query)直接相加,这样的时间复杂度为O(n),第二个问题(update)的时间复杂度为O(1)

方法二:如果我们需要多次的query操作,我们是否有方法可以将降低时间复杂度?这个时候最好的办法就是把这n个整数的前缀和数组求解出来,每一次只需要prefix[right]-prefix[left-1]即可求解出来答案,这样的时间复杂度就降到了O(1),但是这个时候update操作的时间复杂度就升到了O(n),因为我们需要对前缀和数组index之后都进行修改.具体可以参考这篇博客看前缀和相关的内容:Java之前缀和算法_java前缀和算法_允歆辰丶的博客-CSDN博客

因此当我们采用无论哪一种方法,对于一种操作的时间复杂度可能很低,但是对另外一种操作的时间复杂度是很高的,因此是否可以有一种方法,可能将两种操作的时间复杂度平均一下,当然有,就是我们接下来要介绍的线段树,对于两种操作的时间复杂度都为O(log n);

二.线段树

1.什么是线段树

线段树是一种经典的数据结构，用于处理区间查询问题，例如区间求和、区间最小值、区间最大值等。它的基本思想是将区间递归地划分为若干个子区间，并将每个子区间的信息保存在一个节点中，从而形成一棵树形结构，即线段树。

线段树的每个节点都代表一个区间，如果该节点表示的区间与待查询的区间有交集，那么该节点保存的信息就可能对查询有用。因此，在查询时，只需要访问与待查询区间相交的节点即可，而不需要访问整棵树。

线段树通常使用数组来实现，其空间复杂度为 O(n)，其中n是区间的长度。线段树的建树复杂度为 O(n)，单次查询复杂度为 O(\log n)。

2.线段树的举例

我们对数组arr(如下图)构建一颗线段树(如下下图),此时叶子结点就是数组下标为index的值,他们的根结点为叶子结点的之和,一层层向上,根结点为整个数组的和36(也就是index为0到5的和)

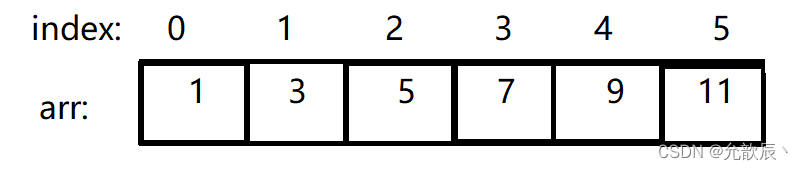
三.构建线段树

1.思路分析

构建一颗线段树可以用数组来模拟树的实现,知道根结点下标(也就是tree数组的node),这个时候它的左子节点为:node_left = node * 2 + 1;右子节点为:node_right = node * 2 + 2;node左节点的对应arr数组的下标范围为[start,mid],node右节点的对应arr数组的下标范围为[mid,end],这个时候我们进行递归创建这个tree数组,我们可以知道递归要到叶子结点,对叶子结点的下标进行赋值,然后再一步步回溯向上对上一层的父节点进行赋值,最后完成对根结点的赋值,所以我们递归的出口为递归到叶子结点,也就是start==end,这个时候赋值 tree[node] = arr[start];

2.代码实现

    public static void buildTree(int[] arr, int[] tree, int node, int start, int end) {if (start == end) {tree[node] = arr[start];return;}int mid = (start + end) / 2;int node_left = node * 2 + 1;int node_right = node * 2 + 2;buildTree(arr, tree, node_left, start, mid);buildTree(arr, tree, node_right, mid + 1, end);tree[node] = tree[node_left] + tree[node_right];}

四.更新

1.思路分析

当我们需要对arr数组中的下标为index的元素进行数值的修改,这个时候也需要对线段树进行更新,例如将下标为3的数值修改为6,这个时候需要递归到下标范围为3的tree数组的下标,然后对值进行修改,然后一层层向上回溯对这半区的树值全部进行修改,我们只需要加上一个范围的判断,选择往左子树递归还是向右子树递归即可

2.代码实现

    public static void updateTree(int[] arr, int[] tree, int node, int start, int end, int index, int val) {if (start == end) {arr[index] = val;tree[node] = val;return;}int mid = (start + end) / 2;int node_left = node * 2 + 1;int node_right = node * 2 + 2;if (index >= start && index <= mid) {updateTree(arr, tree, node * 2 + 1, start, mid, index, val);} else {updateTree(arr, tree, node * 2 + 2, mid + 1, end, index, val);}tree[node] = tree[node_left] + tree[node_right];}

五.查询

1.思路分析

查询代码实现起来是有一定的复杂,首先我们可以先判断返回值为0的情况,也就是需要求和的范围不在当前树的根结点所在的范围内的,一共有两种情况:一种当start>right,一种当left>end,这个时候直接返回0.

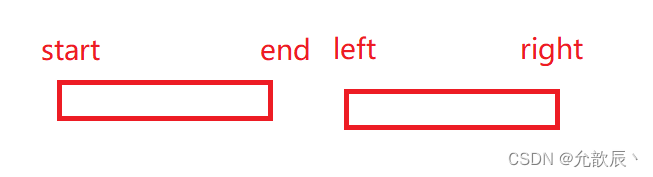
 还有当出现如下图的情况时,直接返回当前结点的值,没必要继续向下递归,因为此时范围全部都符合了

 这个时候最后我们需要把左边的符合范围的和 加上 右边符合范围的和 ,最终的结果就是我们需要求解的范围.

2.代码实现

    /*** * @param arr  原数组* @param tree  构建的tree数组* @param node  根结点在tree数组的下标* @param start 原数组从start索引开始* @param end   原数组到end索引结束* @param left  求和从left索引开始* @param right  到right索引结束的和* @return*/public static int queryTree(int[] arr, int[] tree, int node, int start, int end, int left, int right) {if (right < start || end < left) {return 0;} else if (left <= start && right >= end) {return tree[node];}int mid = (start + end) / 2;int node_left = node * 2 + 1;int node_right = node * 2 + 2;int sum_left = queryTree(arr, tree, node_left, start, mid, left, right);int sum_right = queryTree(arr, tree, node_right, mid + 1, end, left, right);return sum_left + sum_right;}