政府网站建设存在的问题网络推广的含义
电子技术——共栅和共源共栅放大器的高频响应

我们在之前学过无论是是CS放大器还是CE放大器,都可以看做是一个带通(IC低通)滤波器。在高频处的响应收到输入电容 CinC_{in}Cin 的限制(主要是米勒效应)。因此,若想扩大放大器的带宽,我们必须减小米勒效应,一种方案就是共栅放大器。
CG放大器的高频响应
下图展示了CG放大器的高频模型:
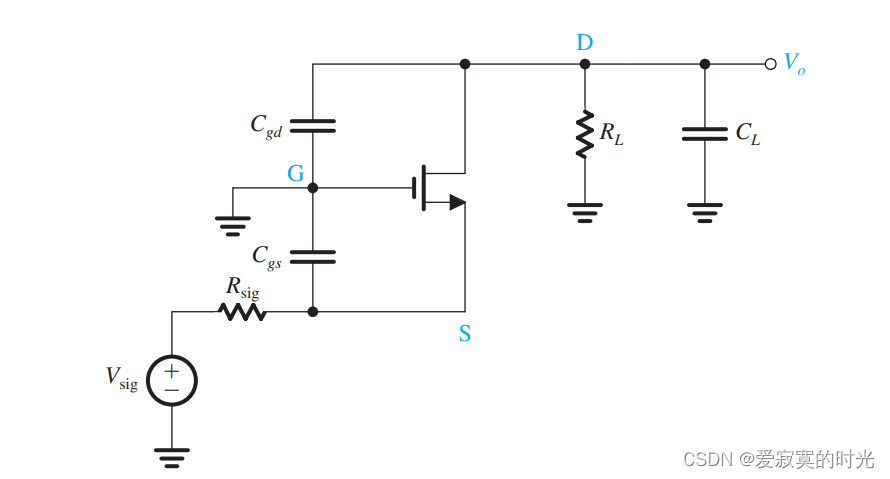
为了一般性,我们在输出端引入了电容 CLC_LCL 表示负载电容,我们发现在CG配置中,我们发现 CgdC_{gd}Cgd 和 CLC_LCL 是并联关系,在以后的分析中我们将其捏合在一起分析。
我们发现上面三个电容,每一个电容的一端都和地相连,因此每一个电容都不是桥路电容,因此不受米勒效应的影响。这说明,CG放大器的带宽要比CS放大器的带宽要宽很多,尤其是输入源阻抗很大的时候。为了分析其高频响应,我们使用T模型分析:
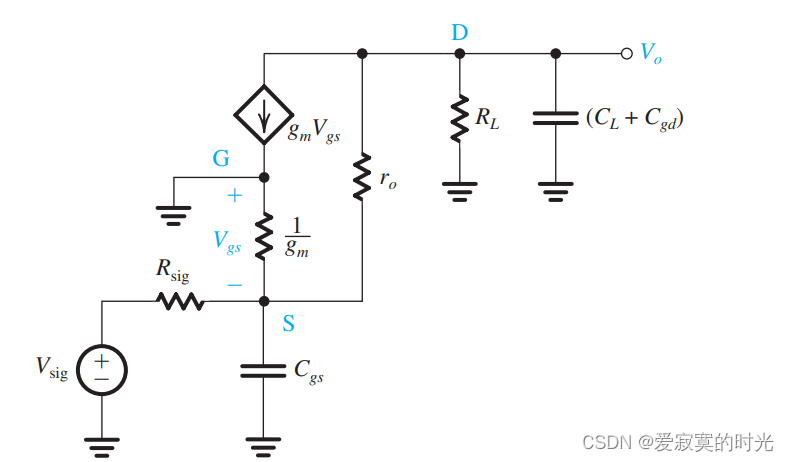
其中,为了方便分析,我们忽略 ror_oro :
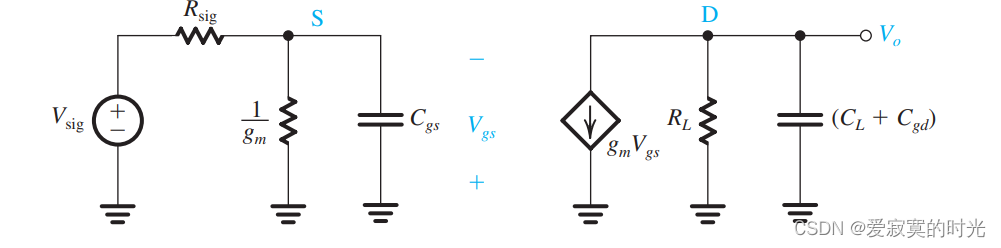
我们知道这个电路应该存在两个极点,对于输入端的低通型STC:
fP1=12πCgs(Rsig∣∣1gm)f_{P1} = \frac{1}{2 \pi C_{gs}(R_{sig}||\frac{1}{g_m})} fP1=2πCgs(Rsig∣∣gm1)1
对于输出端的低通型STC:
fP2=12π(Cgd+CL)RLf_{P2} = \frac{1}{2 \pi (C_{gd} + C_L)R_L} fP2=2π(Cgd+CL)RL1
通常情况下 fP2f_{P2}fP2 要比 fP1f_{P1}fP1 小,因此 fP2f_{P2}fP2 为主导极点。无论怎样说,两个极点都要比CS的极点大,因此CG放大器的具有更大的带宽。
或者,我们可以使用开路时间常数法得到:
fH=12πτH=1/(1fP1+1fP2)f_H = \frac{1}{2 \pi \tau_H} = 1 / (\frac{1}{f_{P1}} + \frac{1}{f_{P2}}) fH=2πτH1=1/(fP11+fP21)
在IC中,必须考虑 ror_oro ,此时我们使用开路时间常数法,首先考虑 CgsC_{gs}Cgs :

得到:
Rgs=Rsig∣∣RinR_{gs} = R_{sig} || R_{in} Rgs=Rsig∣∣Rin
这里的 RinR_{in}Rin 是CG放大器的输入阻抗。
接下来考虑电容 CgdC_{gd}Cgd :
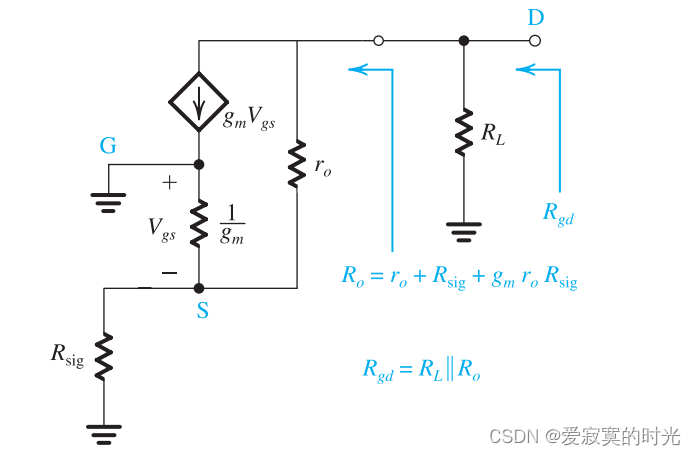
得到:
Rgd=RL∣∣RoR_{gd} = R_L || R_o Rgd=RL∣∣Ro
这里 RoR_oRo 是放大器的输出阻抗(包括 RsigR_{sig}Rsig )。
最后计算 fHf_HfH 即可。
总之,CG放大器的高频响应要比CS放大器优秀,但是由于CG放大器的低输入阻抗,导致整体增益较小。然而,CG可以和CS放大器一起工作,组成共源共栅放大器。
共源共栅放大器的高频响应
下图展示了共源共栅放大器的高频响应模型:
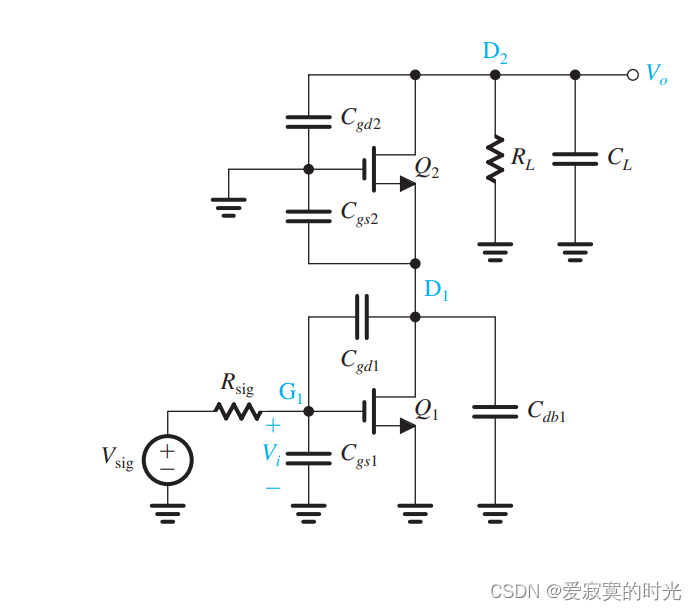
为了估算共源共栅放大器的 fHf_HfH 我们使用开路时间常数法:
- 考虑电容 Cgs1C_{gs1}Cgs1 看到的电阻为 RsigR_{sig}Rsig
- 考虑电容 Cgd1C_{gd1}Cgd1 看到的电容为 Rgd1=(1+gm1Rd1)Rsig+Rd1R_{gd1} = (1 + g_{m1}R_{d1})R_{sig} + R_{d1}Rgd1=(1+gm1Rd1)Rsig+Rd1 其中 Rd1R_{d1}Rd1 是 D1D_1D1 对地的电阻等于 Rd1=ro1∣∣Rin2=ro1∣∣ro2+RLgm2ro2R_{d1} = r_{o1} || R_{in2} = r_{o1} || \frac{r_{o2} + R_L}{g_{m2} r_{o2}}Rd1=ro1∣∣Rin2=ro1∣∣gm2ro2ro2+RL
- 考虑电容 Cdb1C_{db1}Cdb1 和 Cgs2C_{gs2}Cgs2 看到的电阻为 Rd1R_{d1}Rd1
- 考虑电容 CL+Cgd2C_L + C_{gd2}CL+Cgd2 看到的电阻为 RL∣∣RoR_L || R_oRL∣∣Ro 其中 RoR_oRo 是共源共栅放大器的输出电阻 Ro=ro2+ro1+gm2ro2ro1R_o = r_{o2} + r_{o1} + g_{m2}r_{o2}r_{o1}Ro=ro2+ro1+gm2ro2ro1
计算 fHf_HfH 即可。
权衡带宽和增益
为了说明如何权衡带宽和增益,我们观察总体时间常数:
τH=Rsig[Cgs1+Cgd1(1+gm1Rd1)]+Rd1(Cgd1+Cdb1+Cgs2)+(RL∣∣Ro)(CL+Cgd2)\tau_H = R_{sig}[C_{gs1} + C_{gd1}(1 + g_{m1}R_{d1})] + R_{d1}(C_{gd1} + C_{db1} + C_{gs2}) + (R_L || R_o)(C_L + C_{gd2}) τH=Rsig[Cgs1+Cgd1(1+gm1Rd1)]+Rd1(Cgd1+Cdb1+Cgs2)+(RL∣∣Ro)(CL+Cgd2)
首先第一项由共栅放大器的米勒效应贡献,若信号源的内阻较大,此时高频响应由第一项主导。此时想要增加放大器的带宽,我们可以降低负载阻抗 RLR_LRL 进而降低 Rd1R_{d1}Rd1 减小米勒效应。但是若将 RLR_LRL 降低我们知道电压增益也会随之降低。
当 RsigR_{sig}Rsig 较小的时候,第一项的米勒效应就不再是主导因素。此时可以使用较大的 RLR_LRL 来增大电压增益。此时第三项将是主导项,为了进一步说明,我们假设 Rsig=0R_{sig} = 0Rsig=0 并且忽略第二项:
τH≃(CL+Cgd2)(RL∣∣Ro)\tau_H \simeq (C_L + C_{gd2})(R_L || R_o) τH≃(CL+Cgd2)(RL∣∣Ro)
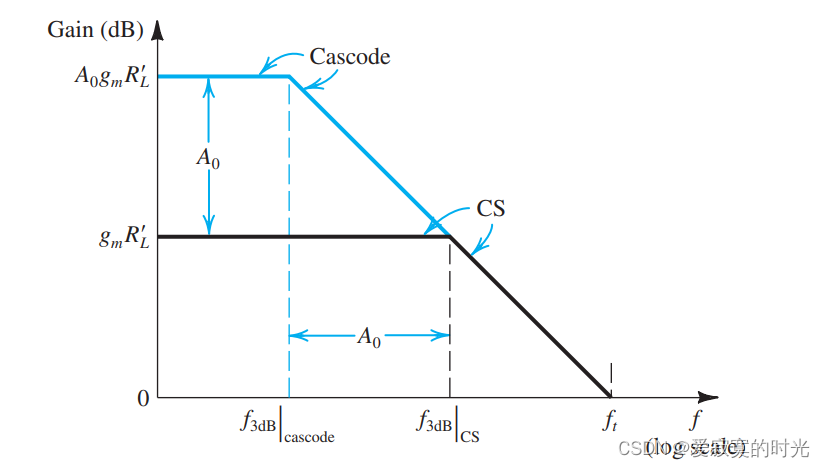
到这里我们就可以和CS放大器比较,如下图:

上图中,我们假设共源共栅放大器中 RL=A0RLR_L = A_0R_LRL=A0RL 我们发现共源共栅放大器的电压增益比CS放大器的大 A0A_0A0 倍,但是 f3dBf_{3dB}f3dB 比 CS放大器小 A0A_0A0 倍。但是单位增益不变。如图:
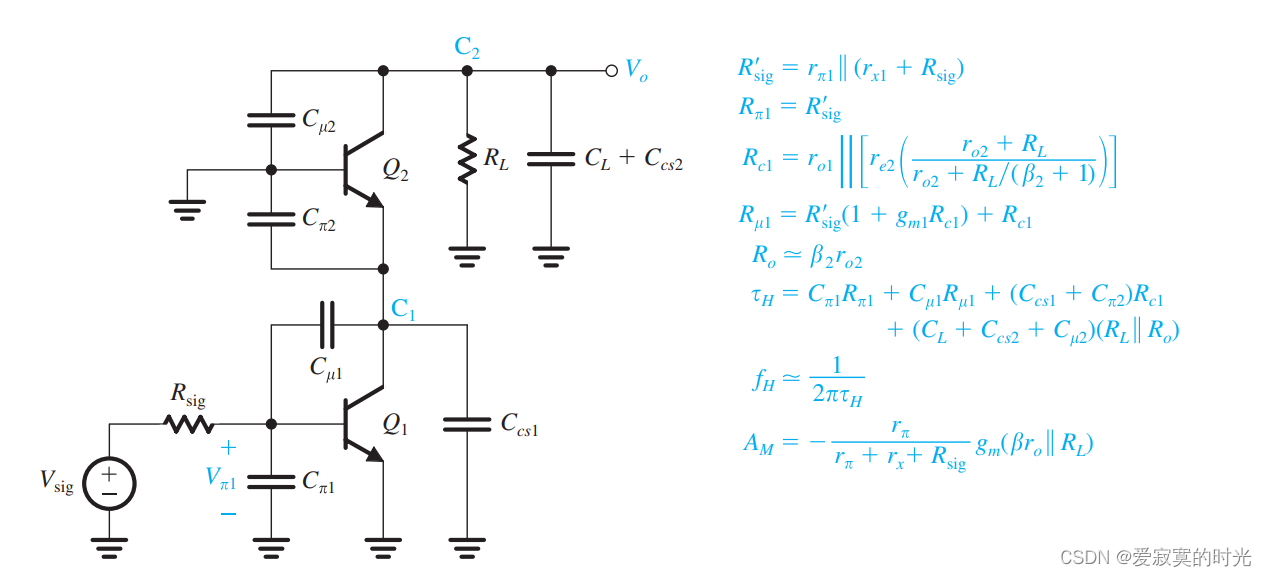
BJT共射共基放大器的高频响应
BJT共射共基放大器的高频响应与MOS的基本一致,如图: