公司网站建设的通知百度官方推广

拟凸（quasi-convex）函数很早就听说过，但是标准定义一直不太了解，现在总结一下。

一个定义在凸集上的实数函数 $f$ 是拟凸函数：若对于其定义域内的任意两个点 $x$ 和 $y$，以及任意常数 $\lambda \in [0,1]$，有
f(λx+(1−λ)y)≤max⁡{f(x),f(y)}f(\lambda x+(1-\lambda)y)\leq \max\{f(x), f(y)\} f(λx+(1−λ)y)≤max{f(x),f(y)}

几何意义是函数任意两点连线上的点，在该函数上的值小于这两点对应函数值的最大值。

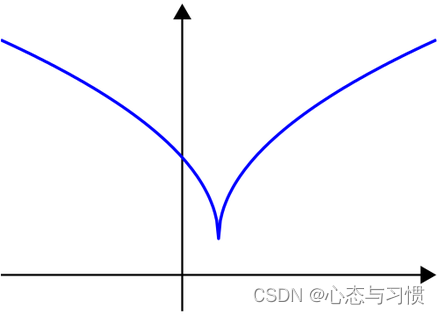
上图就是一个拟凸函数。拟凹函数的定义为：
f(λx+(1−λ)y)≥min⁡{f(x),f(y)}f(\lambda x+(1-\lambda)y)\geq \min\{f(x), f(y)\} f(λx+(1−λ)y)≥min{f(x),f(y)}

正态分布的概率密度函数为一个拟凹函数，如下图所示：

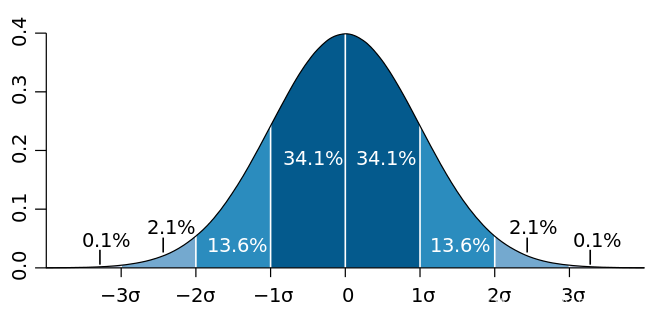
当函数 $f$ 为单变量函数时，单峰函数（只有一个局部极小值或局部极大值的函数）要么是拟凸函数，要么是拟凹函数，而多变量函数时则不一定。

参考资料¹：