东莞设计公司有哪些湖南seo技术培训

1、问题描述

在棋盘上放置 8 个皇后，使得它们互不攻击，此时每个皇后的攻击范围为同行同列和同对角线，要求找出所有解，如下图所示。

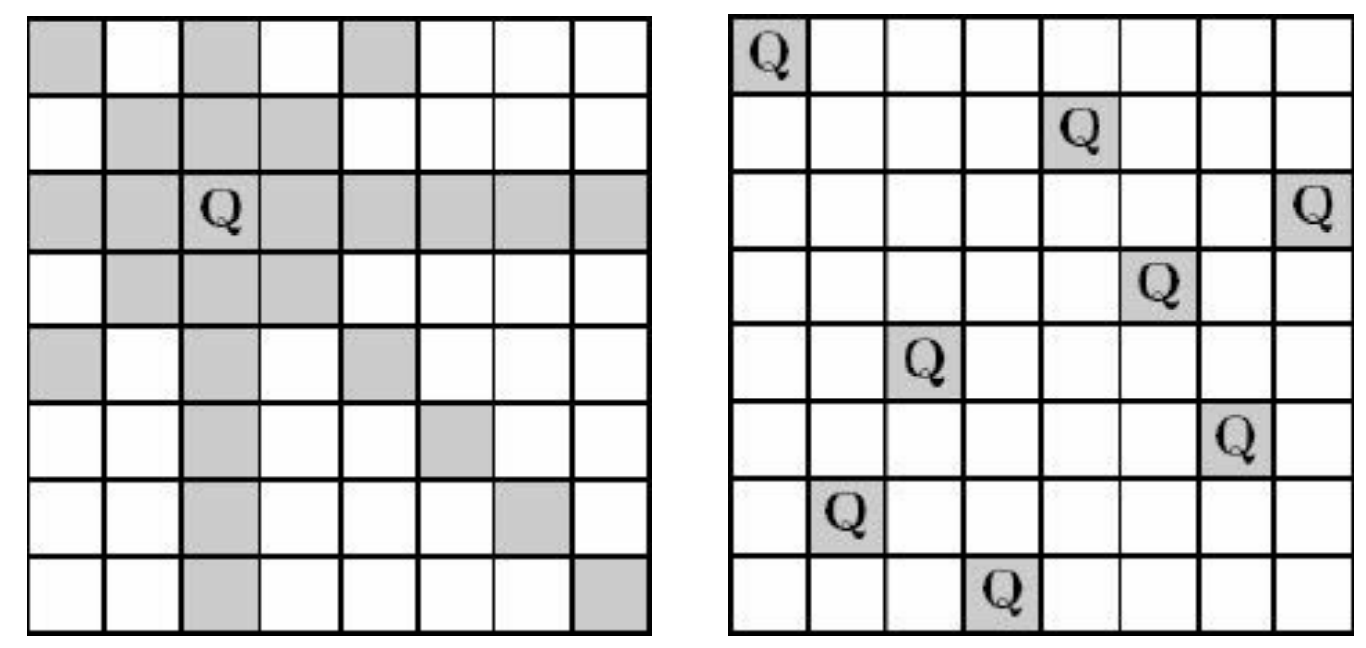
左图为皇后的攻击范围，右图为一个可行解。

2、分析

最简单的思路是把问题转化为 “从 64 个格子中选一个子集”，使得 “子集中恰好 8 个格子，且任意两个选出的格子都不在同一行、同一列或同一个对角线上”。这正是子集枚举问题。然而，64个格子的子集有2⁶⁴ 个，太大了，这并不是一个很好的模型。

第二个思路是把问题转化为 “从 64 个格子中选 8 个格子”，这是组合生成问题。根据组合数学，有 $C_{64}^8=4.426\times 10^9$ 种方案，比第一种方案优秀，但仍然不够好。

经过思考，不难发现以下事实：恰好每行每列各放置一个皇后。如果用 C[x] 表示第 x 行皇后的列编号，则问题变成了全排列生成问题。 而 0 ~ 7 的排列一共只有 8! = 40320个，枚举量不会超过它。

提示：在编写递归枚举程序之前，需要深入分析问题，对模型精雕细琢。一般还应对解答树的结点数有一个粗略的估计，作为评价模型的重要依据，如下图所示。

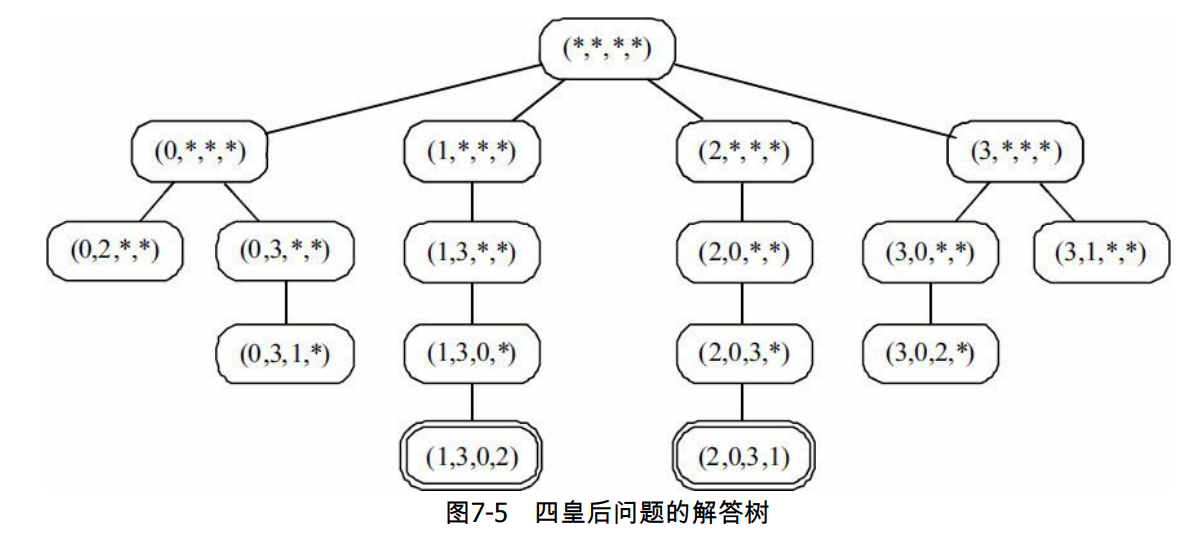
图中给出四皇后问题的完整解答树。它只有 17 个结点，比 4! = 24 小。之所以会这样，是因为有些结点无法继续扩展。如在 (0,2,*,*) 中，第2行无论将皇后放到哪里，都会和第 0 行和第1行中已放好的皇后发生冲突，其他还未放置的皇后更是如此。

在这种情况下，递归函数将不再递归调用它自身，而是返回上一层调用，这种现象称为回溯（backtracking）。

提示：当把问题分成若干步骤并递归求解时，如果当前步骤没有合法的选择，则函数将返回上一级递归调用，这种现象称为回溯。正是因为这个原因，递归枚举算法常被称为回溯法，应用十分普遍。

下面的程序简洁地求解了八皇后问题。在主程序中读入 $n$，并为 $tot$ 清零，然后调用 search(0)，即可得到解的个数 tot。

void search(int cur) {if (cur == n) //递归边界，只要走到了这里，所有皇后必然不冲突tot++; else {for (int i = 0; i < n; i++) {int ok = 1;C[cur] = i; //尝试把第cur行的皇后放到第i列for (int j = 0; j < cur; j++) { //检查是否和前面的皇后冲突if (C[cur] == C[j] || cur - C[cur] == j - C[j] || cur + C[cur] == j + C[j]) {ok = 0;break;}}if (ok) search(cur + 1); //如果合法，继续递归}}
}

注意：既然是逐行放置的，则皇后肯定不会横向攻击，因此只需检查是否纵向和斜向攻击即可。条件 “cur - C[cur] == j - C[j] || cur + C[cur] == j + C[j]” 用来判断皇后 (cur, C[cur]) 和 (j, C[j]) 是否在同一条对角线上。其原理可用下图来说明。

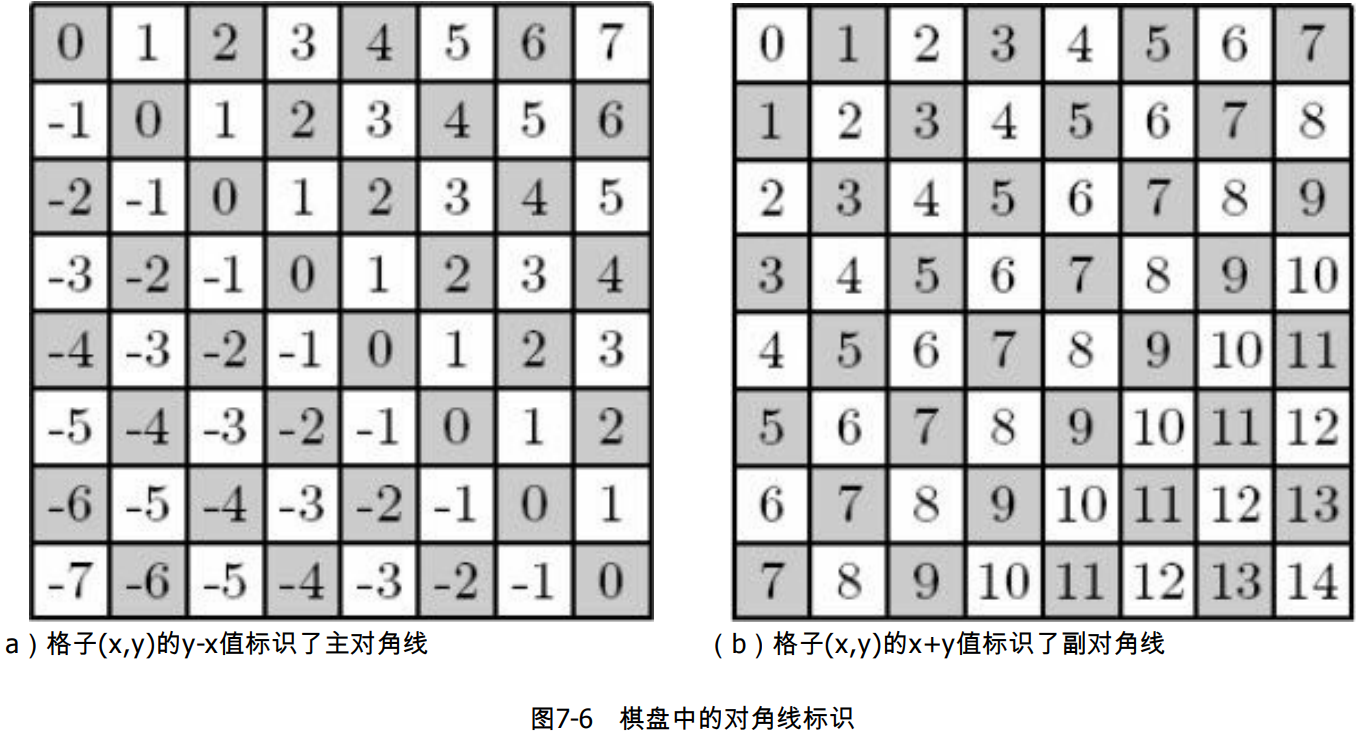
结点数似乎很难进一步减少了，但程序效率可以继续提高：利用二维数组 vis[2][] 直接判断当前尝试的皇后所在的列和两个对角线是否已有其他皇后。注意到主对角线标识 $y-x$ 可能为负，存取时要加上 $n$。

void search(int cur) {if(cur == n) tot++;else {for(int i = 0; i < n; i++) {if(!vis[0][i] && !vis[1][cur+i] && !vis[2][cur-i+n]) { //利用二维数组直接判断C[cur] = i; //如果不用打印解，整个C数组都可以省略vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 1; //修改全局变量search(cur+1);vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 0; //切记！一定要改回来}}}
}

上面程序有个极其关键的地方：vis 数组的使用。vis数组的确切含义：表示已经放置的皇后占据了哪些列、主对角线和副对角线。将来放置的皇后不应该修改这些值——至少“看上去没有修改”。一般地，如果在回溯法中修改了辅助的全局变量，则一定要及时把它们恢复原状（除非故意保留所做修改）。 另外，在调用之前一定要把 vis 数组清空。

提示：如果在回溯法中使用了辅助的全局变量，则一定要及时把它们恢复原状。特别地，若函数有多个出口，则需在每个出口处恢复被修改的值。

3、完整代码

n皇后问题：生成-测试法

#include<cstdio>
using namespace std;int C[50], tot = 0, n = 8, nc = 0;void search(int cur) {int i, j;nc++;if(cur == n) {for(i = 0; i < n; i++)for(j = i+1; j < n; j++)if(C[i] == C[j] || i-C[i] == j-C[j] || i+C[i] == j+C[j]) return;tot++;} else {for(i = 0; i < n; i++) {C[cur] = i;search(cur+1);}}
}int main() {scanf("%d", &n);search(0);printf("%d\n", tot);printf("%d\n", nc);return 0;
}

n皇后问题：普通回溯法

#include<cstdio>
using namespace std;int C[50], tot = 0, n = 8, nc = 0;void search(int cur) {int i, j;nc++;if(cur == n) {tot++;} else { for(i = 0; i < n; i++) {int ok = 1;C[cur] = i;for(j = 0; j < cur; j++) {if(C[cur] == C[j] || cur-C[cur] == j-C[j] || cur+C[cur] == j+C[j]) {ok = 0;break;}}if(ok) search(cur+1);}}
}int main() {scanf("%d", &n);search(0);printf("%d\n", tot);printf("%d\n", nc);return 0;
}

n皇后问题：优化的回溯法

#include<cstdio>
#include<cstring>
using namespace std;int C[50], vis[3][50], tot = 0, n = 8, nc = 0;void search(int cur) {int i, j;nc++;if(cur == n) {tot++;} else for(i = 0; i < n; i++) {if(!vis[0][i] && !vis[1][cur+i] && !vis[2][cur-i+n]) {C[cur] = i;vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 1;search(cur+1);vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 0;}}
}int main() {scanf("%d", &n);memset(vis, 0, sizeof(vis));search(0);printf("%d\n", tot);printf("%d\n", nc);return 0;
}