淘宝客单品网站源码seo优化啥意思

汉诺（Hanoi）塔问题是一个经典的递归问题。

设有A、B、C三个塔座；开始时，在塔座A上有若干个圆盘，这些圆盘自下而上，由大到小地叠在一起。要求将塔座A上的圆盘移到塔座B上，并仍按同样顺序叠放。在移动过程中要求遵守如下规则：

• 每次只能移动一个圆盘；
• 任何时刻都不允许将较大的圆盘压在较小的圆盘之上；
• 在满足前两条规则的前提下，可将圆盘移至A、B、C中任何一塔座上。                                

 

•  例如，3个圆盘的初始状态如下

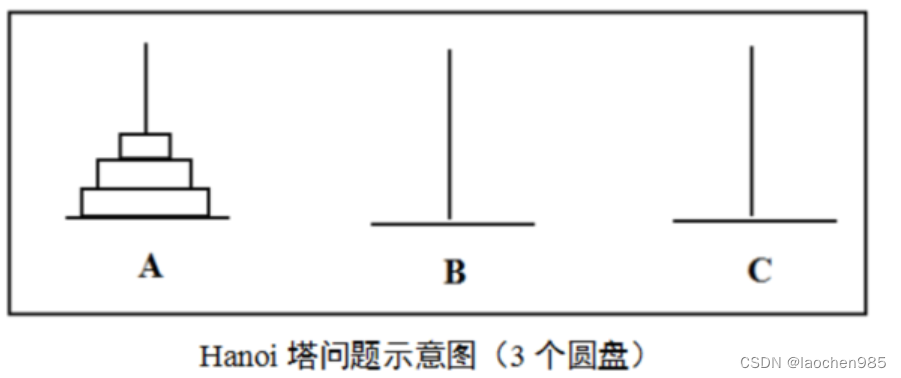
则移动过程如下：
A->B
A->C
B->C
A->B
C->A
C->B
A->B

要求实现一个递归函数，模拟输出n(1<=n<=8)个圆盘从塔座A借助塔座C移动到塔座B上的过程（用A->B表示将圆盘从A移到B，其他类似）。

函数接口定义：

void hanoi(int n, char from, char to, char by);

其中参数 n是圆盘数 、from是原来叠放圆盘的塔座 、to是最终叠放圆盘的塔座 、by是可借助的塔座。

裁判测试程序样例：

#include<iostream>
using namespace std;//将n个圆盘借助by从from移到to
void hanoi(int n, char from, char to, char by);//输入n，输出将原来在A上的n个圆盘借助C移动到B上的移动过程，控制到文件尾
int main() {int n, cnt=0;while(cin>>n) {cnt++;if (cnt>1) cout<<endl;hanoi(n, 'A', 'B', 'C');}return 0;
}

输入样例：

3
4

输出样例：

A->B
A->C
B->C
A->B
C->A
C->B
A->BA->C
A->B
C->B
A->C
B->A
B->C
A->C
A->B
C->B
C->A
B->A
C->B
A->C
A->B
C->B

## 答案：

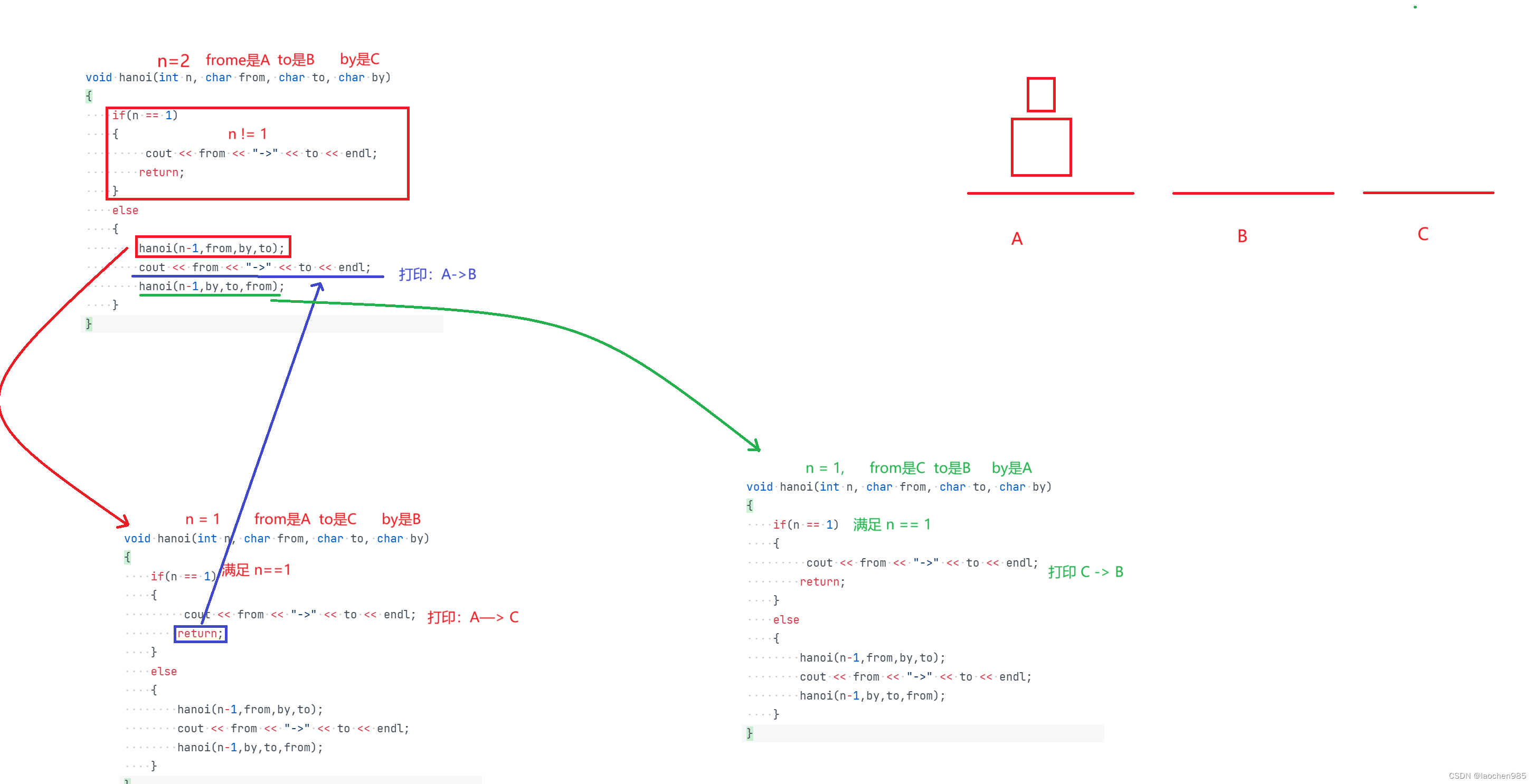
void hanoi(int n, char from, char to, char by)
{if(n == 1){cout << from << "->" << to << endl;return;}else{hanoi(n-1,from,by,to);cout << from << "->" << to << endl;hanoi(n-1,by,to,from);}
}

## 思路：

汉诺塔问题是一个经典的递归问题，它描述了一种将一堆圆盘从一个塔座移动到另一个塔座的问题，同时需要遵守一些规则。问题的规则如下：

1. 有三个塔座，通常称为A、B、C。
2. 初始时，在塔座A上有若干个圆盘，这些圆盘自下而上，由大到小地叠在一起。
3. 目标是将塔座A上的所有圆盘移动到塔座B上，并仍然按照相同的顺序叠放。
4. 每次只能移动一个圆盘。
5. 任何时刻都不允许将较大的圆盘放在较小的圆盘之上。
6. 在满足前两条规则的前提下，可以将圆盘从A、B、C中的任何一个塔座移动到另一个塔座。

汉诺塔问题的目标是找到一种移动方案，将所有圆盘从起始塔座A移动到目标塔座B，中间可以借助辅助塔座C。这个问题可以通过递归算法来解决。

下面是一个详细解释递归函数 hanoi 的实现和工作原理：

void hanoi(int n, char from, char to, char by) {if (n == 1) {cout << from << "->" << to << endl;return;}// 递归步骤：// 1. 将前 n-1 个圆盘从起始塔座(from)经过目标塔座(by)移动到辅助塔座(by)上hanoi(n - 1, from, by, to);// 2. 将最大的圆盘从起始塔座(from)移动到目标塔座(to)上，并输出移动过程cout << from << "->" << to << endl;// 3. 将前 n-1 个圆盘从辅助塔座(by)经过起始塔座(from)移动到目标塔座(to)上hanoi(n - 1, by, to, from);
}

工作原理解释：

1. 如果 n 等于 1，表示只有一个圆盘需要移动，直接将它从 from 移动到 to，并输出移动过程。

2. 如果 n 大于 1，表示有多个圆盘需要移动。递归的过程如下：

   • 第一步：将前 n-1 个圆盘从起始塔座 from 经过目标塔座 to 移动到辅助塔座 by 上。这一步使用了递归调用，因为它也是一个汉诺塔问题，只不过规模减小了。

   • 第二步：将最大的圆盘从起始塔座 from 移动到目标塔座 to 上，并输出移动过程。这是实际的移动步骤。

   • 第三步：将前 n-1 个圆盘从辅助塔座 by 经过起始塔座 from 移动到目标塔座 to 上。这一步同样使用了递归调用。

这个递归过程会一直持续到只剩下一个圆盘需要移动，然后问题就会逐级返回，完成了所有圆盘的移动。

通过这种递归方法，你可以模拟汉诺塔问题的解决过程，并输出移动步骤。