安徽省住房和城乡建设厅官方网站短期职业技能培训班
参考资料:
- DFS 参考文章
- BFS 参考文章
- DFS 参考视频
- 二叉树遍历规律
- 递归原理
- 源码
N叉树规律总结:
由前面二叉树的遍历规律和递归的基本原理,我们可以看到,二叉树遍历口诀和二叉树递推公式有着紧密的联系
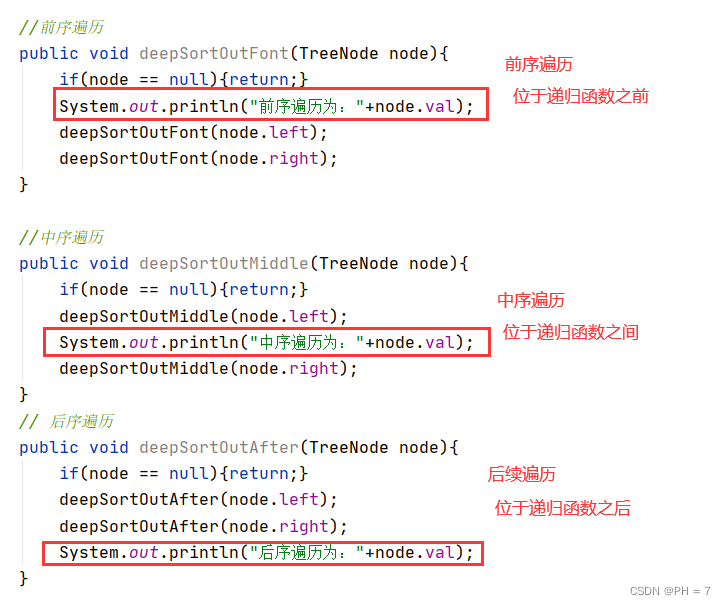
前序遍历:F(x) = op1(x) & F(x左) & F(x右) 口诀:根左右
中序遍历:F(x) = F(x左) & op1(x) &F(x右) 口诀:左根右
后序遍历:F(x) = F(x左) & F(x右) & op1(x) 口诀:左右根
其中op1(x)表示对数据X的操作
如果上述公式中,将op1(x)看做根,可以发现 递推公式和口诀是一摸一样的。
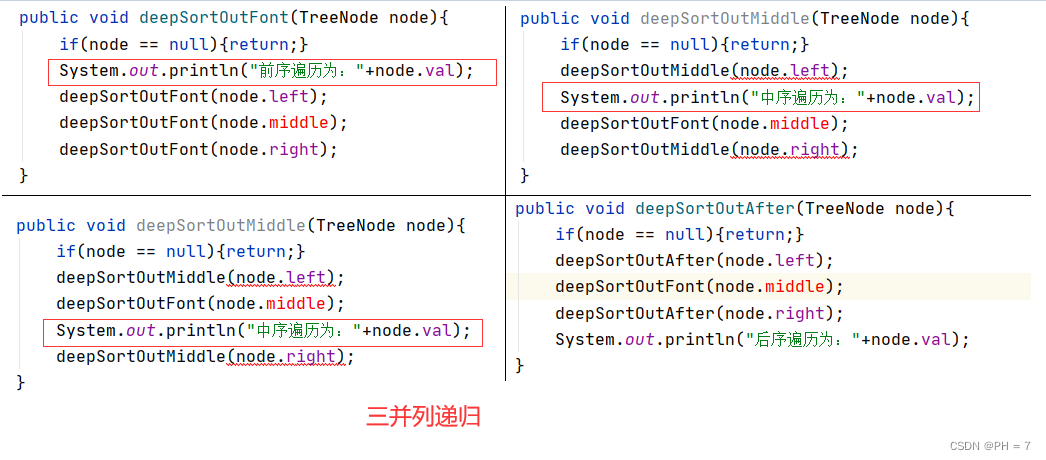
进而我们推断出,3叉树(3并列递归),4叉树(4并列递归)......乃至n叉树(n并列递归)规律都是这样的
3叉树(3并列递归)口诀
公式1:F(x) = op1(x) & F(x左) & F(x中) & F(x右) 口诀:根左中右
公式2:F(x) = F(x左) & op1(x) & F(x中) &F(x右) 口诀:左根中右
公式3:F(x) = F(x左)& F(x中) & op1(x) &F(x右) 口诀:左中根右
公式4:F(x) = F(x左)& F(x中) &F(x右) & op1(x) 口诀:左中右根
其中op1(x)表示对数据X的操作
4叉树(4并列递归)口诀
公式1:F(x) = op1(x) & F(x上) & F(x下) & F(x左) & F(X右) 口诀:根上下左右
公式2:F(x) = F(x上) & op1(x) & F(x下) & F(x左) & F(X右) 口诀:上根下左右
公式3:F(x) = F(x上) & F(x下) & op1(x) & F(x左) & F(X右) 口诀:上下根左右
公式4:F(x) = F(x上) & F(x下) & F(x左) & op1(x) & F(X右) 口诀:上下左根右
公式5:F(x) = F(x上) & F(x下) & F(x左) & F(X右) & op1(x) 口诀:上下左右根
其中op1(x)表示对数据X的操作
扩展至n叉树(n并列递归)口诀
公式1:F(x) = op1(x) & F(x属性1) & F(x属性2) & ......&F(x属性n)
口诀:根,属性1,属性2,......,属性n
N叉树规律验证:
由上述总结出的n叉树规律
公式1:F(x) = op1(x) & F(x属性1) & F(x属性2) & ......&F(x属性n)
口诀:根,属性1,属性2,......,属性n
我们用以下三叉树来进行验证,分别进行前中后序三种遍历
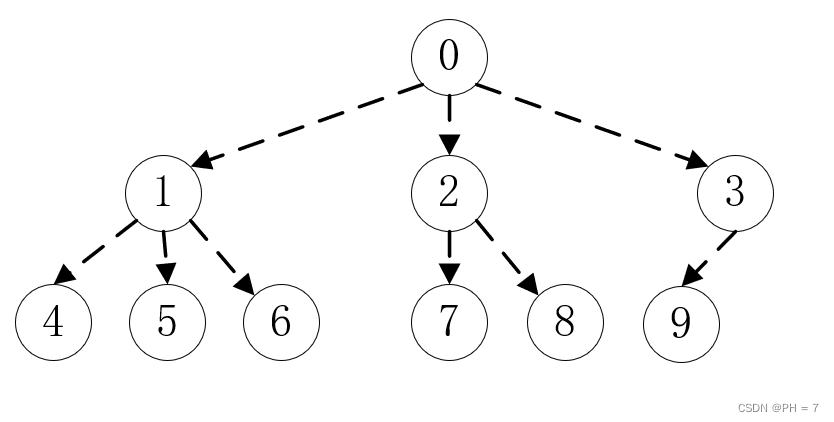
初始化语句:
//对三叉树进行初始化public TreeNode initNode(){// 先初始化最底层的TreeNode node9 = new TreeNode(9,null, null, null);TreeNode node8 = new TreeNode(8,null, null, null);TreeNode node7 = new TreeNode(7,null, null, null);TreeNode node6 = new TreeNode(6,null, null, null);TreeNode node5 = new TreeNode(5,null, null, null);TreeNode node4 = new TreeNode(4,null, null, null);TreeNode node3 = new TreeNode(3,node9, null, null);TreeNode node2 = new TreeNode(2,null, node7, node8);TreeNode node1 = new TreeNode(1,node4, node5, node6);TreeNode node0 = new TreeNode(0,node1, node2, node3);return node0;}- 前序遍历
根据代码:
public void deepSortOutFont(TreeNode node){if(node == null){return;}System.out.println("前序遍历为:"+node.val);deepSortOutFont(node.left);deepSortOutFont(node.middle);deepSortOutFont(node.right);}得到公式以及遍历口诀:
F(x) = op1(x) & F(x左) & F(x中) & F(x右) 口诀:根左中右
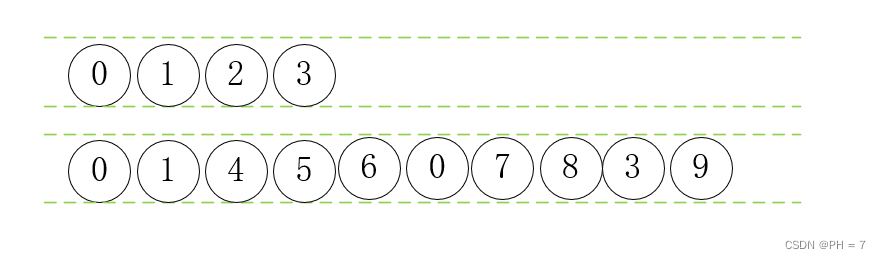
- 从根节点开始,根据口诀:根左中右,得到结果:0,1,2,3
- 以未遍历的节点1为根,根据口诀:根左中右,即1,4,5,6,得到结果:0,1,4,5,6,2,3
- 以未遍历的节点2为根,根据口诀:根左中右,即2,null,7,8,得到结果:0,1,4,5,6,2,7,8,3
- 以未遍历的节点3为根,根据口诀:根左中右,即3,9,null,null,得到结果:0,1,4,5,6,2,7,8,3,9
- 以未遍历节点4,5,6,7,8,9为根,根据口诀:根左中右,即n,null,null,null值不计,结果不变
- 所以根据递推公式总结的口诀:得到遍历结果为:,1,4,5,6,2,7,8,3,9
然后我们执行程序
@Testpublic void test(){//首先进行初始化TreeNode headNode = initNode();//深度优先遍历deepSortOutFont(headNode);//deepSortOutMiddle(headNode);//deepSortOutAfter(headNode);// 广度优先遍历//layerTranverse(headNode);}得到结果:

程序执行结果和口诀推导得到的结果一致,验证成功
总结:n项并列递归理解以及向非递归的转化:
- 根据代码总结出递推函数
对于一个n项递归函数,我们可以很轻易的写出他的递推函数,例如一个归并排序

mearge函数的意思是,将数组的left下标到right下标进行倒序排序,这里为了方便说明就不写出,文章后面会贴出完整代码
得到递推函数:
F(array,left,right) = op1 & F(array,left,middle) & F(array,middle,right) & op2
op表示数据操作,
F(array,left,middle) 为 F(array,left,right)的左半部分
F(array,middle,right) 为 F(array,left,right)的右半部分
- 根据递推函数得到遍历口诀
拆分公式,确保每一个公式只有一个op操作,并得到遍历口诀
F(array,left,right) = op1 & F(array,left,middle) & F(array,middle,right) 口诀:根左右
F(array,left,right) = F(array,left,middle) & F(array,middle,right) & op2 口诀:左右根
- 例举样本数据,从根节点开始,以未遍历的节点为根,按照遍历口诀,对各个节点进行排序
创建样本数据
array:{ 5, 4, 9, 8, 7, 6, 0, 1, 3, 2 }
left:0
right: 9
画出二叉树(当然三并列就是三叉树,n并列就是n叉树)
根据函数表述:两个递归函数是将数组的左半部分和右半部分不断分解,直到left>=right(注意终止条件不画出),得到如下二叉树
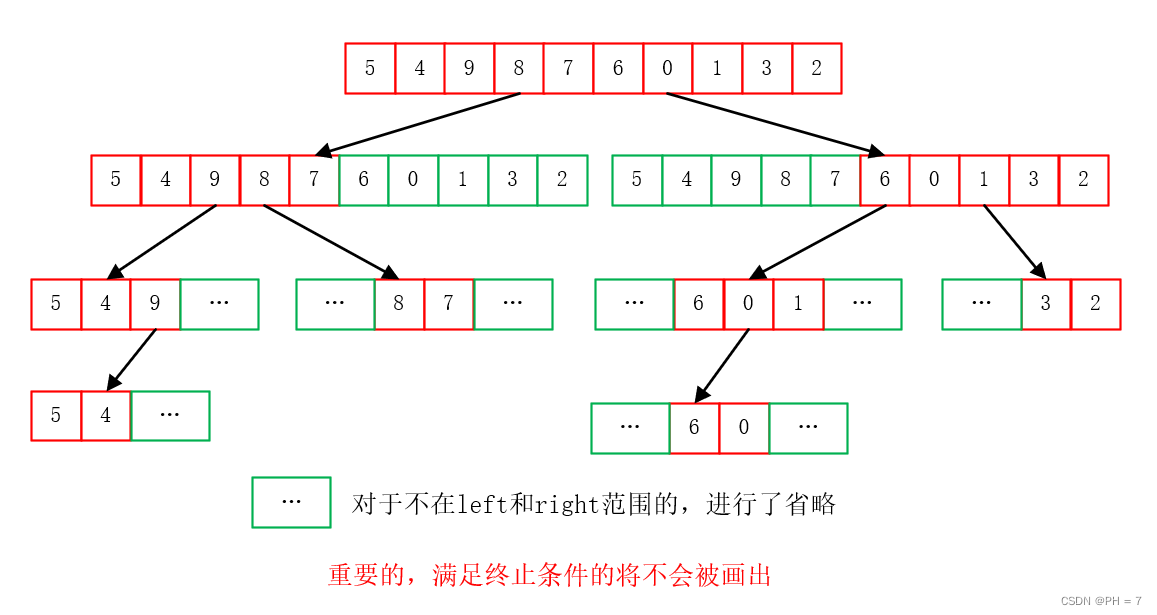
以第二个公式为例:
F(array,left,right) = F(array,left,middle) & F(array,middle,right) & op2 口诀:左右根
从根节点开始,根据:左右根口诀,得到merge函数的入参顺序,根据merge定义:将下标范围内的数字进行倒序排列,得到每一次入参后的结果
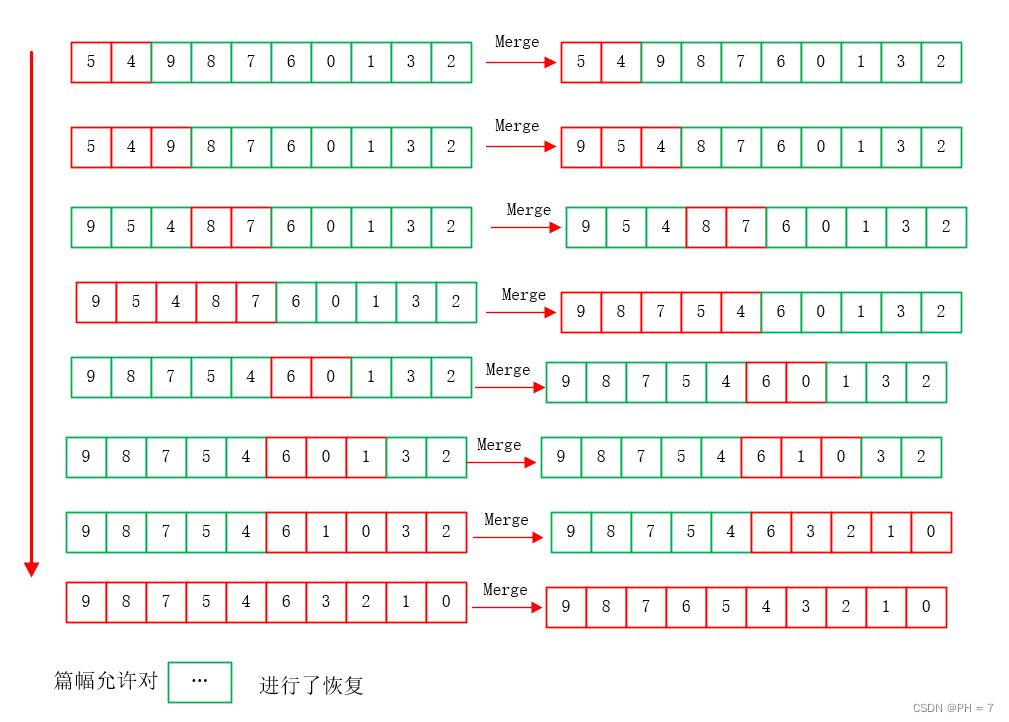
- 将排序后的数据依次作为数据操作函数的入参,归纳总结出该递推函数的作用
根据二叉树的分解以及执行流程,理解了此归并排序的含义:将数组不断地利用二分法进行分解,直至两个元素,然后再对每一部分进行排序
- 并且将循环套用的递归函数转化为了线性的,有多个入参的操作函数,且总结出递归函数的执行顺序
深度、广度优先遍历
其实,二叉树的深度,层级遍历,对应的就是简易的深度、广度优先遍历,见上一级
下面将简单介绍下他们在二维数组中的应用,以岛屿问题为例
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
深度优先遍历的解决办法是:详情见
void dfs(int[][] grid, int r, int c) {// 判断 base caseif (!inArea(grid, r, c)) {return;}// 如果这个格子不是岛屿,直接返回if (grid[r][c] != 1) {return;}grid[r][c] = 2; // 将格子标记为「已遍历过」// 访问上、下、左、右四个相邻结点dfs(grid, r - 1, c);dfs(grid, r + 1, c);dfs(grid, r, c - 1);dfs(grid, r, c + 1);
}// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}其实就是4并列递归
广度优先遍历的遍历方法为:详情见
// 网格结构的层序遍历
// 从格子 (i, j) 开始遍历
void bfs(int[][] grid, int i, int j) {Queue<int[]> queue = new ArrayDeque<>();queue.add(new int[]{r, c});while (!queue.isEmpty()) {int n = queue.size();for (int i = 0; i < n; i++) { int[] node = queue.poll();int r = node[0];int c = node[1];if (r-1 >= 0 && grid[r-1][c] == 0) {grid[r-1][c] = 2;queue.add(new int[]{r-1, c});}if (r+1 < N && grid[r+1][c] == 0) {grid[r+1][c] = 2;queue.add(new int[]{r+1, c});}if (c-1 >= 0 && grid[r][c-1] == 0) {grid[r][c-1] = 2;queue.add(new int[]{r, c-1});}if (c+1 < N && grid[r][c+1] == 0) {grid[r][c+1] = 2;queue.add(new int[]{r, c+1});}}}
}
其实就是二叉树层级遍历的变形
