经典的全连接神经网络

经典的全连接神经网络来包含四层网络：输入层、两个隐含层和输出层，将手写数字识别任务通过全连接神经网络表示，如 图3 所示。

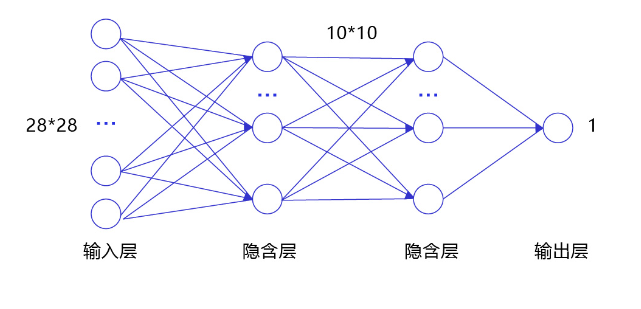
图3：手写数字识别任务的全连接神经网络结构

• 输入层：将数据输入给神经网络。在该任务中，输入层的尺度为28×28的像素值。
• 隐含层：增加网络深度和复杂度，隐含层的节点数是可以调整的，节点数越多，神经网络表示能力越强，参数量也会增加。在该任务中，中间的两个隐含层为10×10的结构，通常隐含层会比输入层的尺寸小，以便对关键信息做抽象，激活函数使用常见的Sigmoid函数。
• 输出层：输出网络计算结果，输出层的节点数是固定的。如果是回归问题，节点数量为需要回归的数字数量。如果是分类问题，则是分类标签的数量。在该任务中，模型的输出是回归一个数字，输出层的尺寸为1。

---

说明：

隐含层引入非线性激活函数Sigmoid是为了增加神经网络的非线性能力。

举例来说，如果一个神经网络采用线性变换，有四个输入$x_1$~$x_4$，一个输出$y$。假设第一层的变换是$z_1=x_1-x_2$和$z_2=x_3+x_4$，第二层的变换是$y=z_1+z_2$，则将两层的变换展开后得到$y=x_1-x_2+x_3+x_4$。也就是说，无论中间累积了多少层线性变换，原始输入和最终输出之间依然是线性关系。

---

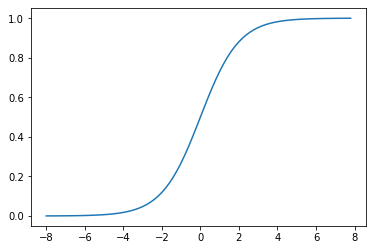
Sigmoid是早期神经网络模型中常见的非线性变换函数，绘制出Sigmoid的函数曲线。

卷积神经网络

虽然使用经典的全连接神经网络可以提升一定的准确率，但其输入数据的形式导致丢失了图像像素间的空间信息，这影响了网络对图像内容的理解。对于计算机视觉问题，效果最好的模型仍然是卷积神经网络。卷积神经网络针对视觉问题的特点进行了网络结构优化，可以直接处理原始形式的图像数据，保留像素间的空间信息，因此更适合处理视觉问题。

卷积神经网络由多个卷积层和池化层组成，如 图4 所示。卷积层负责对输入进行扫描以生成更抽象的特征表示，池化层对这些特征表示进行过滤，保留最关键的特征信息。

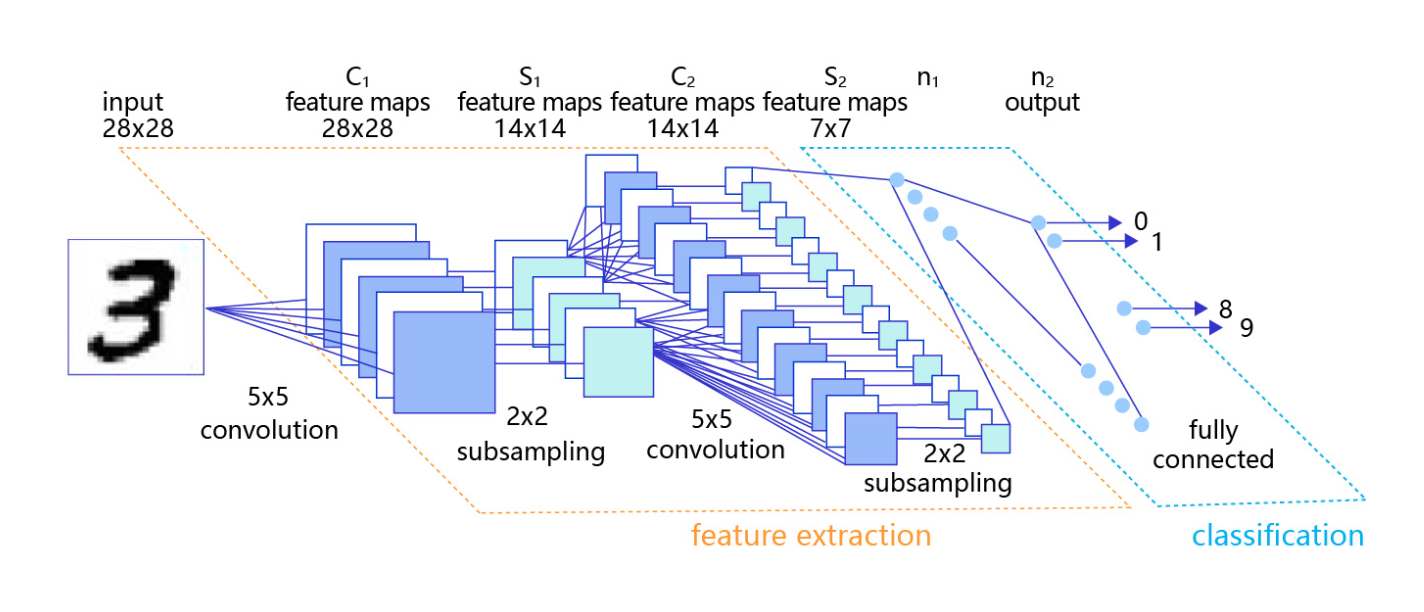
图4：在处理计算机视觉任务中大放异彩的卷积神经网络

---

说明：

本节只简单介绍用卷积神经网络实现手写数字识别任务，以及它带来的效果提升。读者可以将卷积神经网络先简单的理解成是一种比经典的全连接神经网络更强大的模型即可，更详细的原理和实现在接下来的《计算机视觉-卷积神经网络基础》中讲述。

---

两层卷积和池化的神经网络实现如下所示。

# 定义 SimpleNet 网络结构
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):def __init__(self):super(MNIST, self).__init__()# 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层，池化核的大小kernel_size为2，池化步长为2self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)# 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层，池化核的大小kernel_size为2，池化步长为2self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)# 定义一层全连接层，输出维度是1self.fc = Linear(in_features=980, out_features=1)# 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出# 卷积层激活函数使用Relu，全连接层不使用激活函数def forward(self, inputs):x = self.conv1(inputs)x = F.relu(x)x = self.max_pool1(x)x = self.conv2(x)x = F.relu(x)x = self.max_pool2(x)x = paddle.reshape(x, [x.shape[0], -1])x = self.fc(x)return x

使用MNIST数据集训练定义好的卷积神经网络，如下所示。

---

说明：
以上数据加载函数load_data返回一个数据迭代器train_loader，该train_loader在每次迭代时的数据shape为[batch_size, 784]，因此需要将该数据形式reshape为图像数据形式[batch_size, 1, 28, 28]，其中第二维代表图像的通道数（在MNIST数据集中每张图片的通道数为1，传统RGB图片通道数为3）。

#网络结构部分之后的代码，保持不变
def train(model):model.train()#调用加载数据的函数，获得MNIST训练数据集train_loader = load_data('train')# 使用SGD优化器，learning_rate设置为0.01opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())# 训练5轮EPOCH_NUM = 10# MNIST图像高和宽IMG_ROWS, IMG_COLS = 28, 28loss_list = []for epoch_id in range(EPOCH_NUM):for batch_id, data in enumerate(train_loader()):#准备数据images, labels = dataimages = paddle.to_tensor(images)labels = paddle.to_tensor(labels)#前向计算的过程predicts = model(images)#计算损失，取一个批次样本损失的平均值loss = F.square_error_cost(predicts, labels)avg_loss = paddle.mean(loss)#每训练200批次的数据，打印下当前Loss的情况if batch_id % 200 == 0:loss = avg_loss.numpy()[0]loss_list.append(loss)print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, loss))#后向传播，更新参数的过程avg_loss.backward()# 最小化loss,更新参数opt.step()# 清除梯度opt.clear_grad()#保存模型参数paddle.save(model.state_dict(), 'mnist.pdparams')return loss_listmodel = MNIST()
loss_list = train(model)